2D-2D特征点匹配法计算相机运动

2D-2D特征点匹配法计算相机运动

一.基础知识

在介绍通过2D图像之间的特征点匹配计算相机运动之前，不得不介绍一下相关的基础知识，主要包括相机成像的原理，针孔相机模型以及齐次坐标系的介绍。

1.相机成像原理

首先，我们来看一下一张照片是如何拍出来的，下面是一个单反相机。

我们将该相机的主要结构抽象出来，如下所示。

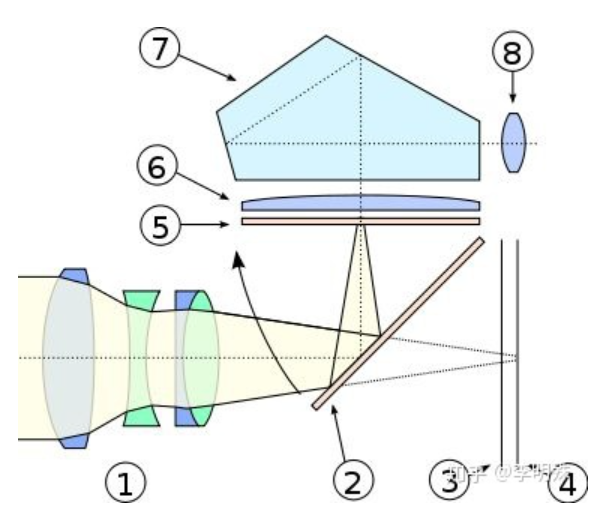
我们的拍照过程通常是这样：找到一个合适的角度，通过取景器⑧观察画面，当画面符合我们要求时，按下快门，就完成了拍照的过程。

以上这个简单的拍照过程，主要包含两个步骤，一是取景，二是按快门。我们在做这两个动作的时候发生了什么呢？

首先是取景，光线通过镜头①射到反光镜②上，然后反射到五棱镜⑦上，通过五棱镜的反射，光线到达取景器⑧,我们通过观察取景器就能看到我们要拍的画面。

然后是按快门，在按快门之前，反光镜位于②位置，用于反射光线以便我们取景，当我们按下快门的瞬间，反光镜从②拉到⑤，这样光线就直接射到传感器③上，照片就形成了。

二.相机模型

相机将三维世界的坐标点映射到二维图像平面的过程可以用一个几何模型来描述，我们称这个模型为相机模型。相机模型有很多种，最简单的是针孔相机模型。

针孔相机模型背后的原理就是小孔成像原理，我们来复习一下小孔成像原理，通过下面这个实验来唤醒大家的记忆。

上面这个实验我们可以观察到，F形状的光源发射的光线通过中间的带有小孔的挡板，在最右侧的成像板上形成一个倒立的F图像。

我们可以通过小孔成像模型来解释针孔相机模型。将模型抽象得到下图。

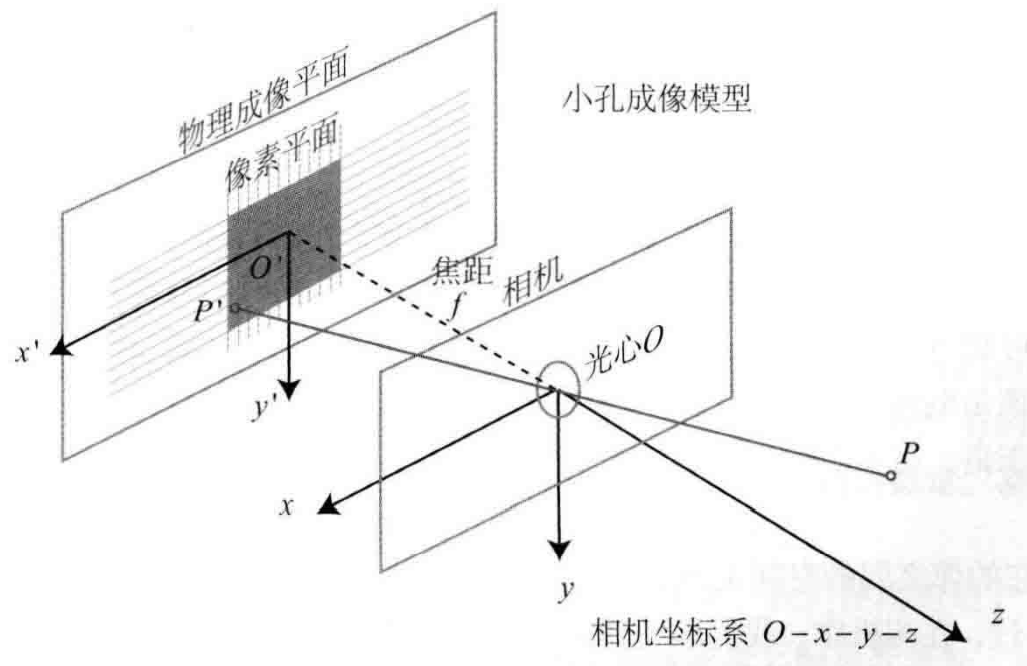
其中P是世界中真实的点，P`是P在二维图像中的投影点。

针孔相机模型总共包括4个坐标系，分别是像素坐标系、图像坐标系、相机坐标系和世界坐标系

像素坐标系：以图像平面左上角为原点的坐标系，X轴和Y轴分别平行于图像坐标系的X轴和Y轴。用（u,v）表示其坐标值。
图像坐标系：以光心在图像平面投影为原点的坐标系，X轴和Y轴分别平行于图像平面的两条垂直边，用（x`,y`）表示其坐标值。图像坐标系是用物理单位表示像素在图像中的位置。
相机坐标系：以相机光心为原点的坐标系，X轴和Y轴分别平行于图像坐标系的X轴和Y轴，相机的光轴为Z轴，用(x,y,z)表示其坐标值。
世界坐标系：是三维世界的绝对坐标系，我们需要用它来描述三维环境中的任何物体的位置，用(xw,yw,zw)表示其坐标值。

我们研究这个针孔相机模型的目的就是为了确定P`和P之间的几何关系。

设P在相机坐标系下的坐标为（X,Y,Z）,P`在图像坐标系下的坐标为（X‘，Y‘，Z‘）,我们最后想得到的是像素坐标系下的P‘和相机坐标系下的P之间的关系。

首先，我们通过相机模型可以得到一个相似三角形

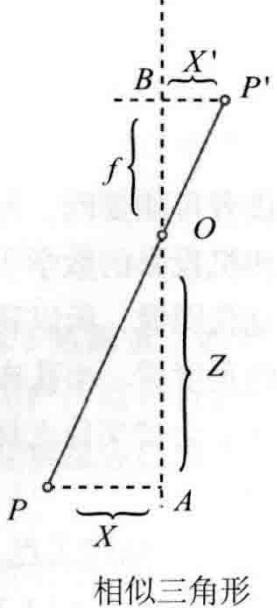
其中f是焦距（光心到成像平面中心的距离），根据相似三角形的关系，我们可以得到

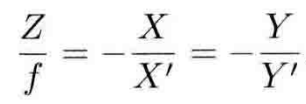
其中负号表示成像是倒立的。为了方便，我们将成像平面根据光心做中心对称。

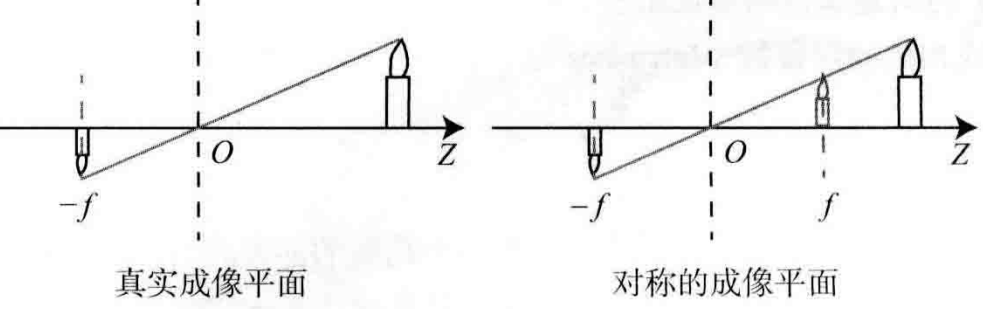
得到如下关系：

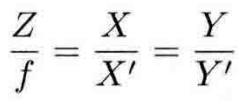
整理得

像素坐标系下的P‘和图像坐标系下的P‘的关系

已知P‘点在图像坐标系上的坐标，求P‘点在像素坐标系上的坐标。

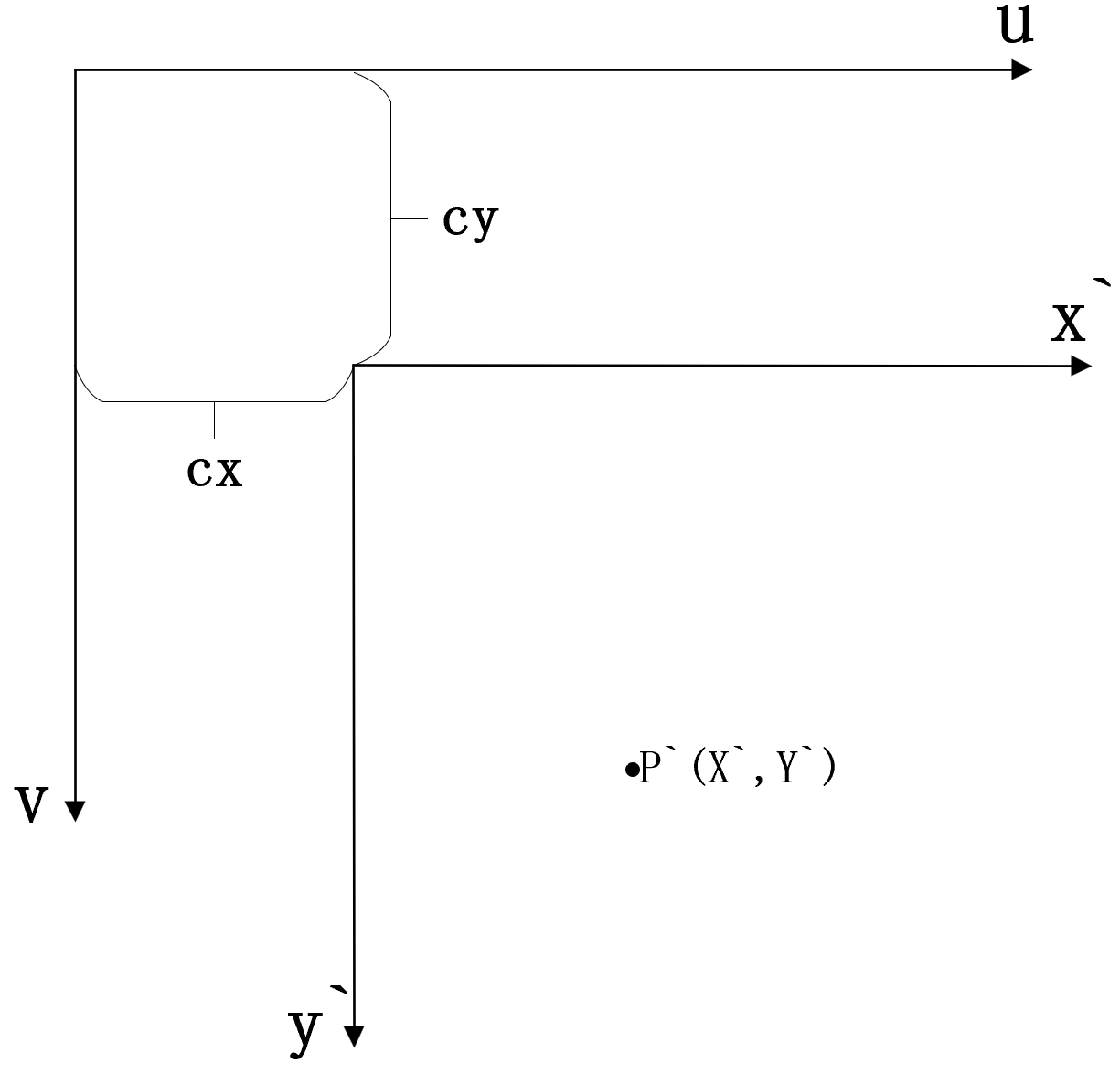
其中，cx和cy表示图像坐标原点到像素坐标原点的位移（单位为像素），α和β分别表示图像坐标系中x轴和y轴每单位有多少个像素，单位为（像素/米）。

像素坐标系下的P‘和相机坐标系下的P之间的关系

结合式（5,3）,把αf合并为fx，βf合并为fy，（5,4）式可转化为相机坐标系中的P点和其在像素坐标系上的投影点P`之间的关系

把（u,v）用转成齐次坐标并将上式写成矩阵形式

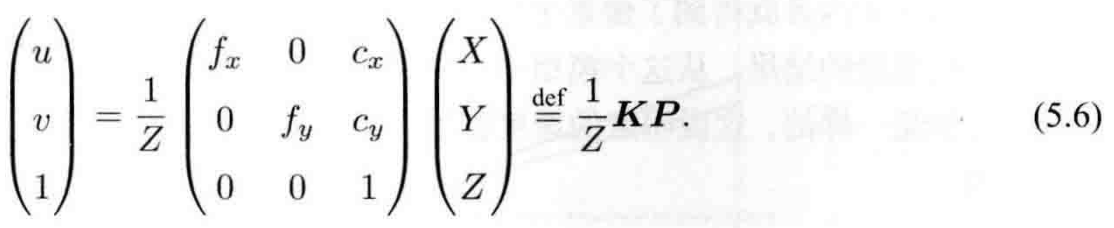
其中K=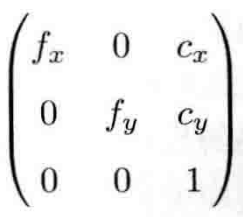称为相机的内参

将5.6式中1/Z的值并入（X,Y,Z)^T向量，相当于P点在相机坐标系下的坐标(X,Y,Z)除以Z，即（X/Z,Y/Z,1)，我们称这个坐标为P点在归一化平面上的坐标。从而我们得到了像素坐标系下的P`和归一化平面上P的关系：即归一化平面上P的坐标左乘相机内参K就得到了像素坐标系下的P’。

三.对极几何

这部分，我们将介绍真实世界中的点与相机在不同视角下成像的对应点之间的几何约束关系。

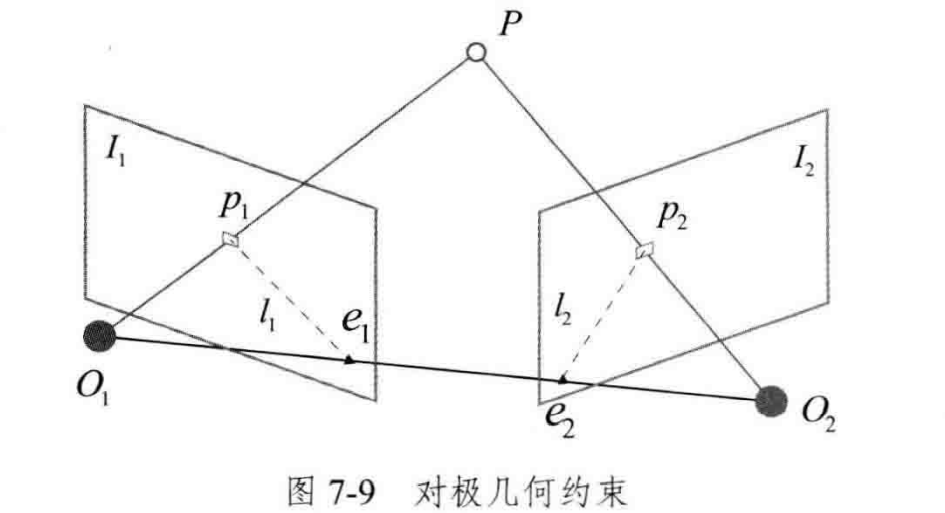
上图P是真实世界的点，p1是相机光心位于O1时，P点投影到投影平面I1上的对应点，同理，p2是相机光心位于O2时，P点投影到投影平面I2上的对应点。

连接O1和O2，连线和两个投影面的交点e1,e2称为极点。

O1PO2三点构成的平面称为极平面。

极平面与投影平面的相交线称为极线。

当我们不知道p1在投影平面I2上的对应点p2时，我们就无法确定P的具体位置，但我们可以知道P一定在O1与p1连接线射线上，也可以确定极平面，通过极平面我们可以确定极线，虽然我们无法确定p2的具体位置，但我们可以知道p2一定在极线上。

1.p1和p2之间的几何约束

当相机光心位于O1时，即相机坐标系原点位于O1时，设P在相机坐标系下坐标为（X,Y,Z)。通过第二部分介绍的内容，我们可以知道p1和P之间的几何关系为

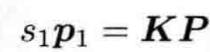
记为式（5.7），其中s1就是Z。

当相机光心位于O2时，O1到O2的变换关系为O2=RO1+t，其中R代表旋转，t代表平移。所以有

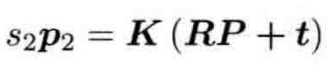
记为式（5.8），其中，假设相机坐标系原点位于O2时，且P在相机坐标系下坐标为（X2,Y2,Z2)，则s2就等于Z2，现在为了使相机坐标系统一，将O2的相机坐标系映射到O1，已知两个相机坐标系的变换关系，O2是O1通过旋转变换R和平移变换t得到的，所以（X2,Y2,Z2）=R(X,Y,Z)+t。

设P在相机坐标系O1的归一化平面上的坐标为x1，则由p1与x1关系为

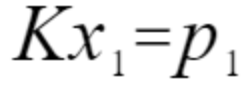
同理设P在相机坐标系O2的归一化平面上的坐标为x2，则p2与x2关系为

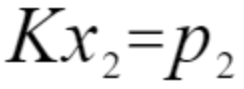
代入式5.7和式5.8得

整理得

5.11两边同乘t^，即两边同时和t做外积得

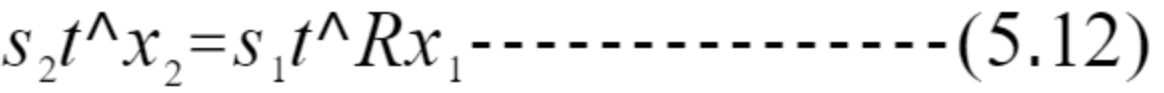
式5.12两边同乘x2^T,即两边同时和x2做内积得

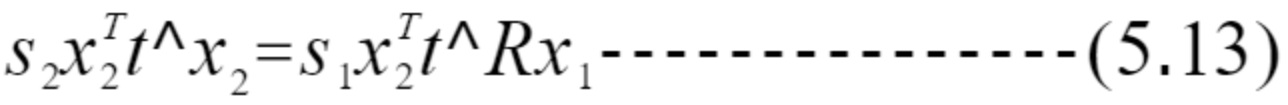
因为t和x2的外积t^x2同时垂直于t和x2，所以5.12式左侧与x2的内积为0，则有

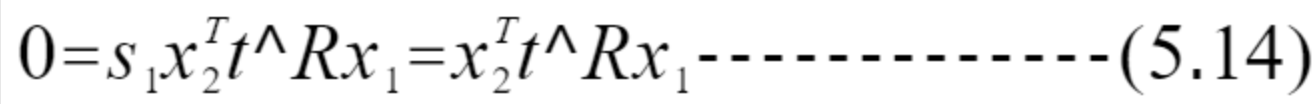
重新代入p1和p2得式5.15

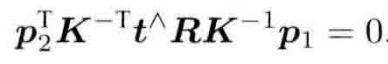
我们把t^R记作基础矩阵F，把式5.15中间部分即为本质矩阵E，得到对极约束

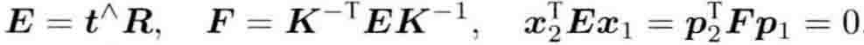
由此，我们可以得到相机位姿估计问题求解步骤

1.根据配对点的像素坐标求出E或者F（八点法）
2.根据E或F求出R,t

如果已知相机内参K，外参R和t，我们就可以求出本质矩阵E和基础矩阵F（在实际应用中，由于相机参数的测量误差以及图像中的噪声等因素，计算出的本质矩阵可能会存在误差。）。在图像配准深度学习方法中，使用带有相机内参K，外参R和t的数据集，我们就可以使用E或者F作为监督信号，步骤如下

1.通过深度学习模型得到两幅图像的特征点对
2.通过特征点对的像素坐标求出E或者F(八点法)
3.将得到和E或者F与通过数据集自带参数K，R，t计算得到的E或者F计算损失。